
This is a short version of a recent article [1] about "pseudospherical" surfaces. These were extensively studied in the nineteenth century and are now, because of connections with integrable systems, having a minor revival.
These surfaces are equally "saddle-shaped" at each point. The product
of their two curvatures at each point is -1 everywhere. So in a sense
they are the opposite (or hyperbolic counterpart) of an ordinary sphere.
Here is the simplest one:

One nice thing about these surfaces is that they can be covered by coordinates known as "Tchebyshev nets." To physically construct a Tchebyshev net, take a piece of non-stretch fabric which is loosely woven so that the angle between the threads can change. Now drape it over the surface so that the warp and weft of the fabric become coordinate lines on the surface. Perhaps it should be called a Tchebyshev fishing net to emphasize that the knots don't move.
Actually, any surface can be locally covered by a Tchebyshev net.
The classic reference is
[2]--it sounds like
M. Tchébichef gave a good seminar, but it's a pity that this original
treatment was never published in more detail. His india rubber ball
may have looked something like this

The connection is that on a pseudo-spherical surface, the lines
of a Tchebyshev net have more special properties: they have constant
torsion (three-dimensionality), and their
normals are tangent to the surface
everywhere:
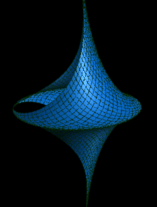
Most importantly, the angle between them
obeys the famous "sine-Gordon" equation

This equation has an amazingly rich
mathematical structure, known as "complete integrability," which
allows the construction of lots of pseudo-spherical surfaces...
The screw

Deep Space Nine

The pseudosphere awakes

The manta ray

The Edward Weston Memorial Calla Lily

[1] Robert McLachlan, A gallery of constant-negative-curvature surfaces, Mathematical Intelligencer, Fall 1994, 31-37.
[2] P. L. Tchebyshev, Sur la coupe des vêtements (1878), Oeuvres II, Chelsea 1962.
Visualizations were done in geomview, available from
the Geometry Center.
Back to the IFS home page.