I'm interested in the broad area of dynamical systems. Lately my research has focussed on understanding the dynamics of piecewise-smooth differential equations and maps which are used to model phenomena with nonsmooth features such as impacts in mechanical systems and switching in electrical systems and control systems. Below are some specific topics.

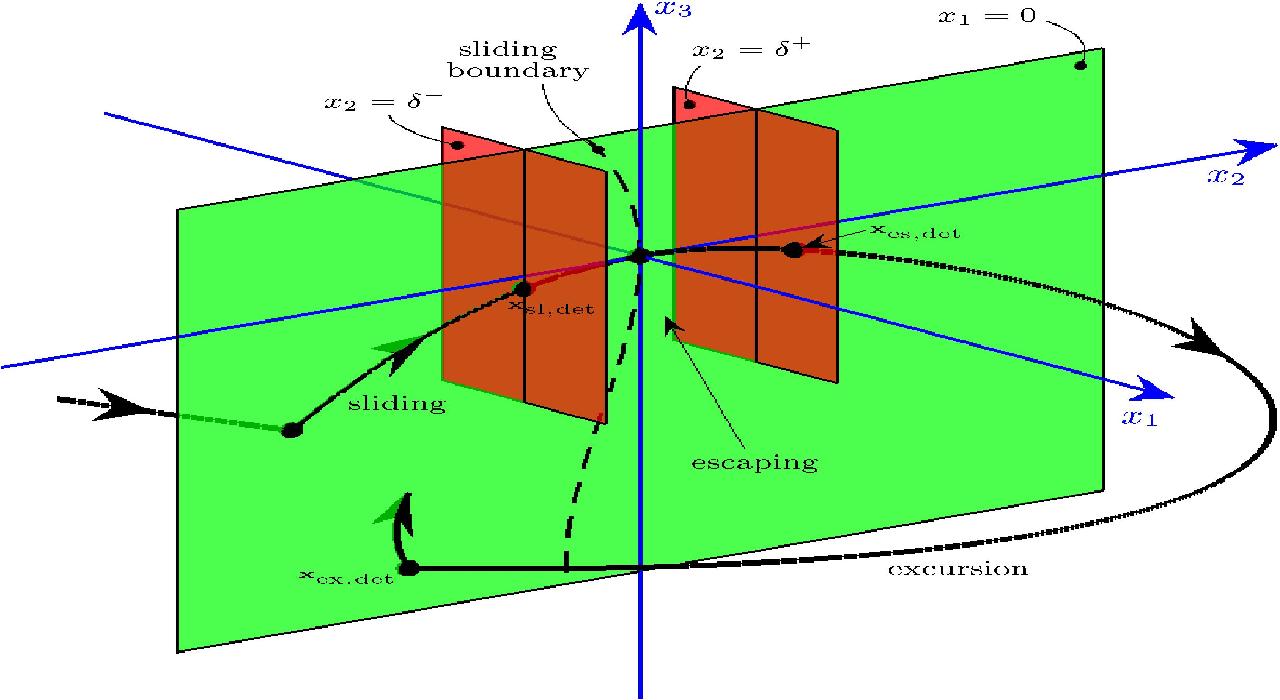
Stochastically perturbed sliding motion.
Trajectories evolve on switching manifolds of discontinuous vector fields whenever the vector field on both sides of the manifold points towards the surface. This is known as sliding motion. As shown below, the addition of a small amount of randomness in the form of Brownian motion pushes sample trajectories off the switching manifold, but large excursions are curbed by the deterministic component of the system.

Periodic orbits with sliding motion have been described in relay control models and ecological models. It is interesting that small noise can have large qualititative effects on the oscillatory motion and we'd like to understand the mechanisms that cause this for periodic orbits with sliding.

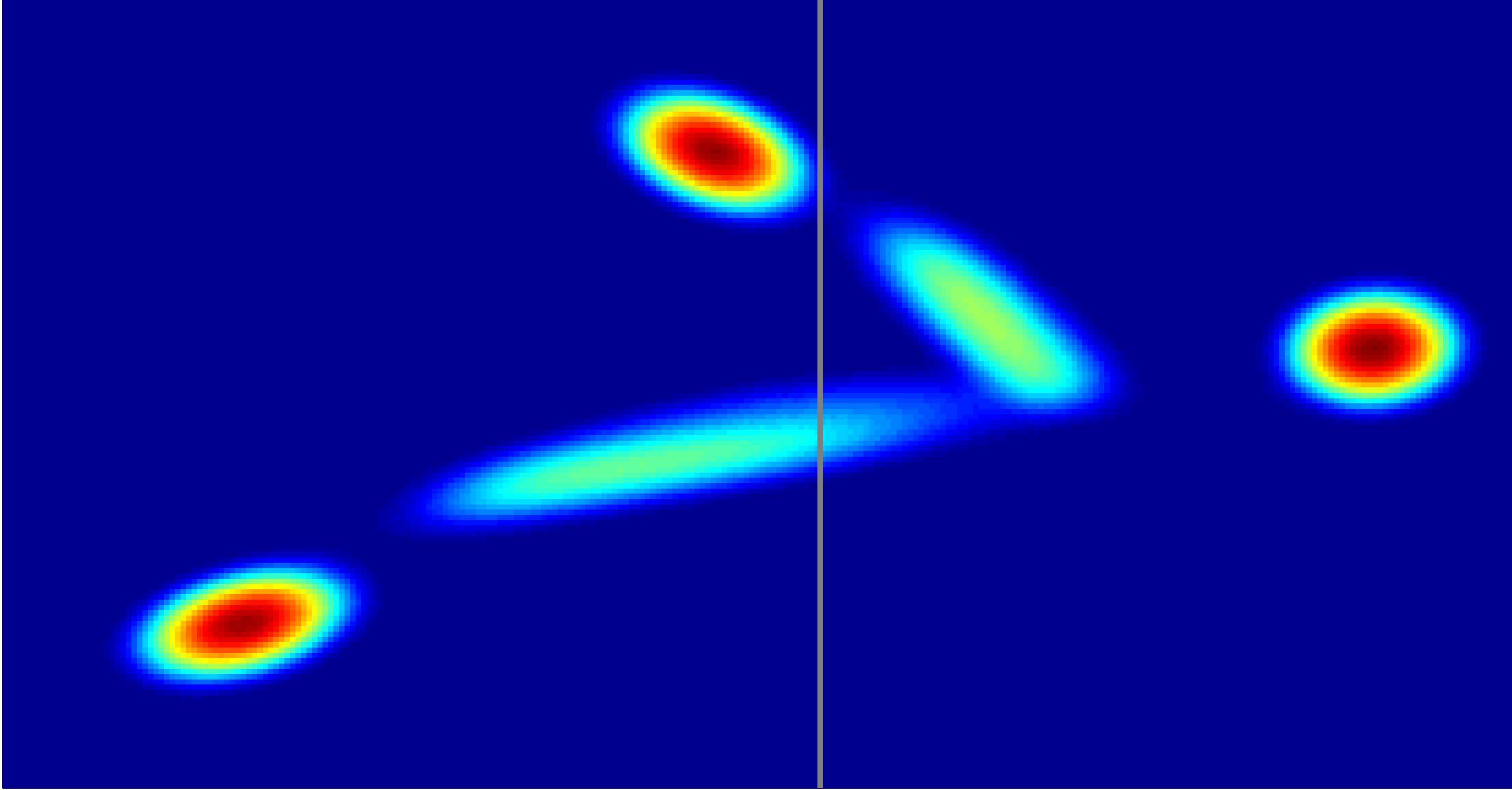
Stochastic grazing bifurcations.
A grazing bifurcation occurs when a periodic orbit collides with a switching manifold. For vibro-impacting systems this corresponds to the onset of recurring impacts. The figure below depicts a two-dimensional invariant probability density function of a return map for a typical grazing bifurcation with small noise. Remarkably the size of invariant density (and thus the deviations in the oscillatory motion) may be proportional to the square-root of the noise amplitude as a consequence of the extreme nonlinearity of impact events.

Arnold tongues in piecewise-smooth, continuous maps.
Oscillators subject to external forcing may be entrained to a rational multiple of the forcing frequency. Regions of parameter space for which this occurs are known as Arnold tongues. The figure below shows Arnold tongues for a piecewise-linear, continuous map (different colours correspond to different periods). We have a good understanding of the distinctive chain structure of the tongues but it remains to properly explain many other features, such as the small sequence visible in the lower right and the creation of chaotic solutions.

Balancing by time-delayed, switching control.
Balance is a prototypical control problem relating to, for instance, human postural sway, human balancing tasks and walking robots. A key feature of mathematical models of balance is the presence of time-delay corresponding to the time between when the individual or machine performing the control measures variables and applies corrective forces. Switching control laws are relevant because this may be easier to implement mechanically and muscles tend to move intermittently. However, the combination of time-delay and switching makes the mathematics rather complicated.